Learning Objectives
This section focuses on:
- Relative atomic atomic mass and relative formula mass
- Empirical and molecular formula
- The mole as the unit of amount
- Molar mass
- Molar concentration
- Avogadro’s Law
Part 1: Relative Atomic Mass
Relative Atomic Mass (Ar) is the weighted average mass of an atom of an element compared to 1/12th the mass of a carbon-12 atom. It takes into account the different isotopes of the element and their abundances.
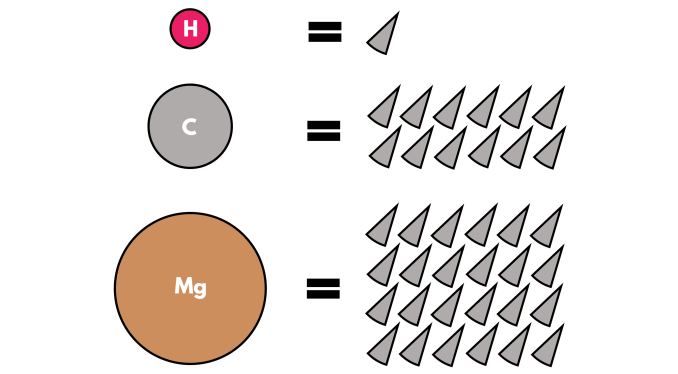
From the above, it is noted that hydrogen has a unit mass of 1 whilst magnesium has a unit mass of 24. This was then used as the standard i.e starting point of assigning mass for all atoms. Carbon unit mass is 12. This number now is used. Therefore, when comparing with magnesium mass, two moles of carbon would balance a scale with one mole of magnesium. Since carbon weighs 12 units, magnesium is 12 * 2 = 24.
Modern atomic studies is now using mass spectrometer which gives the relative abundances of isotopes of an element.

It is often found on the periodic table and is not necessarily a whole number because it accounts for isotope distribution.
Part 2: Empirical and molecular formula
Example Calculation of Empirical
Step 1: Find the Empirical Formula
Let’s say a compound contains 40% carbon (C), 6.7% hydrogen (H), and 53.3% oxygen (O) by mass.
- Step 1: Convert mass percentages to moles:

- Step 2: Divide by the smallest number of moles:

- Step 3: Rewrite the elements as a compouns with its subscript ratio:
So, the empirical formula is CH₂O.
Example Calculation of Empirical
Suppose the molecular mass of the compound is 180 g/mol.
Step 1: Find the molar mass of the empirical formula (CH₂O):
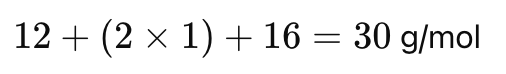
Step 2: Determine the multiple:

Step 3: Multiply the empirical formula by 6:
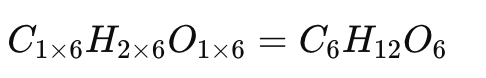
Step 4: Rewrite the elements as a compound with its molecular ratio:
So, the molecular formula is C₆H₁₂O₆ (which is glucose).
Part 3: Mole Concept

Concept 1: Mass and moles


Activity 1: Watch this video answer the following questions together with the video
- Example 1: Find the amount of 30.0 g of Li3TaO4
- Example 2: Find the mass of 0.003 mol of KMnO4
Concept 2: Number of particles and moles
Avogadro’s Constant (NA):
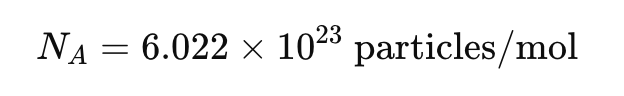
This means that 1 mole of any substance contains 6.02×1023 particles (atoms, molecules, or ions).

Question: Find the number of molecules in 2 moles of water (H₂O)
Answer:
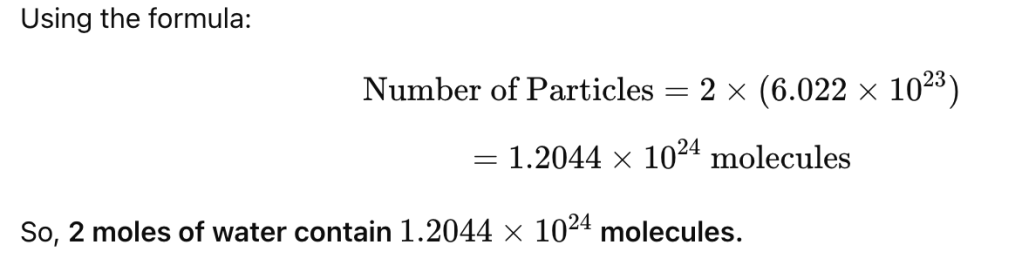
Subscribe to get access: Find the number of moles if a sample contains 3.011×1023 atoms of carbon.
Read more of this content when you subscribe today.
Concept 3: Concentration (solution) and moles
Concentration of solution is expressed in many different units including:
- Molarity (mol / dm3)
- Molality (mol / Kg)
- Part per million (ppm)
- Density (g/cm3)
In the IB, molarity is the one that is used.
- Molarity = the amount of solute (in moles) in 1 dm3 of solvent (pure water)
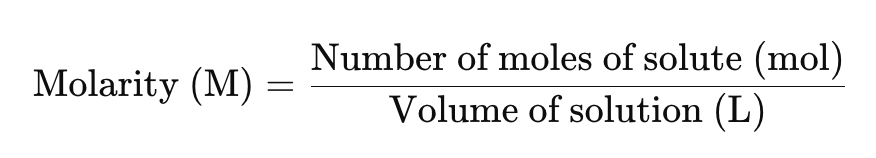
Note that the unit of volume is L or dm3. These two are the same factor i.e 1 L = 1 dm3

Subscribe to get access: Find the number of moles in 250 mL of a 0.5 mol/L of NaCl solution.
Read more of this content when you subscribe today.
Activity 2: Watch this video to explore further about finding the limiting reactant
- Example: Find the mass of CO2 produed when 250 cm3 of 0.1 mol/dm3 of HCl reacts with 1.8 g of CaCO3
Concept 4: Volume of gas at STP and moles
Volume of Gas at STP and Moles
At Standard Temperature and Pressure (STP):
- Temperature = 0°C (273.15 K)
- Pressure = 1 atm (101.3 kPa)
- 1 mole of any ideal gas occupies 22.4 liters (L or dm3)
- Formula: Volume of gas (L or dm3) = Moles × 22.4
Formula to Find Moles from Volume at STP:
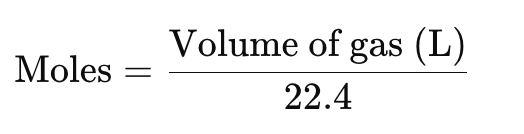
Question: Find the volume of 3 moles of oxygen (O₂) gas at STP
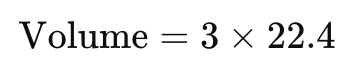
Subscribe to get access: Find the number of moles in 44.8 dm3 of nitrogen (N₂) gas at STP.
Read more of this content when you subscribe today.
Volume of Gas at SATP and Moles
At Standard Ambient Temperature and Pressure (SATP):
- Temperature = 25°C (298.15 K)
- Pressure = 1 atm (101.3 kPa)
- 1 mole of any ideal gas occupies 24 liters (dm3)
This has the same concept as STP but with different volume occupied by the gas. This is consistent with the relation of temperature and volume. Higher temperature would increase air pressure hence a gas in a container would occupy a larger volume
Activity 3: Use Ideal Gas equation, PV = nRT
- Example: Find the volume of CO2 produced when 250 cm3 of 0.1 mol/dm3 of HCl reacts with 1.8 g of CaCO3 at 100 kPa and 280 K

![ESS 8.1.3 [AHL] Biocapacity and Environmental Migration](https://mypytrclass.com/wp-content/uploads/2025/12/image-4.png?w=1024)




![ESS 8.3.4 [AHL] Photochemical Smogs and Tropospheric Ozone](https://mypytrclass.com/wp-content/uploads/2025/12/image-1.png?w=1024)
